|
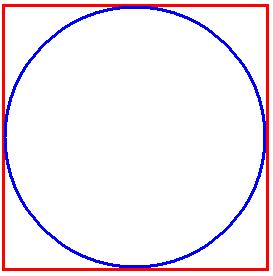
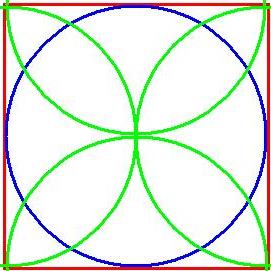
Further to the previous two pages about MT 137, I was searching for conclusive evidence that Bessler got the idea about the ‘circles of fifths’ from Johann Heinichen and I stumbled on an interesting feature of the dodecagram which in my opinion supplies more evidence that MT 137 can only be interpreted as a pointer to the number 5. It seemed to me that Bessler must have been taught about the ‘circle of fifths’ while learning how to build organs. It is said that the creation and use of the ‘Circle of Fifths’ is the very foundation of Western music theory. Along with all the technical things the Circle predicts, it is also described as a musician’s best friend in the world, in deciphering key signatures on sight. Apparently it is just as essential in writing music because its clever design is very helpful in composing and harmonizing melodies, building chords, and moving to different keys within a composition. The circle of fifths gets its name from the fact that you travel across the circle from one point to another 5/12ths of the way around it. If you draw a line each time you link two keys you end upo with a dodecagram. It is inconceivable that Bessler was unaware of the term ‘circle of fifths’ as a musician and organ maker nor how to read the circle of fifths - and equally unlikely that he would not make the connection of the word ‘fifths’ with his own encoded material which is full of references to the number five. Given the close proximity both in time and place, of the man most associated with the scheme, Johann Heinichen, and Bessler’s work on organs it is equally unbelievable that the two men did not know each other. I’m certain that Bessler deliberately included MT 137 as a clue to the number 5. So in an effort to resolve my problem I sought information about how the circle of fifths was taught. There is a big clue in the way you construct a dodecagram I had never considered how Bessler drew this geometric figure, and there is more than one way to achieve it, however the one I’m about to describe is fascinatingly relevant to my quest and is simple to construct requiring nothing more than a ruler and compass. Start by drawing a circle and create a square round it, as in the picture below. The circle will form the outer edge of the dodecagram.
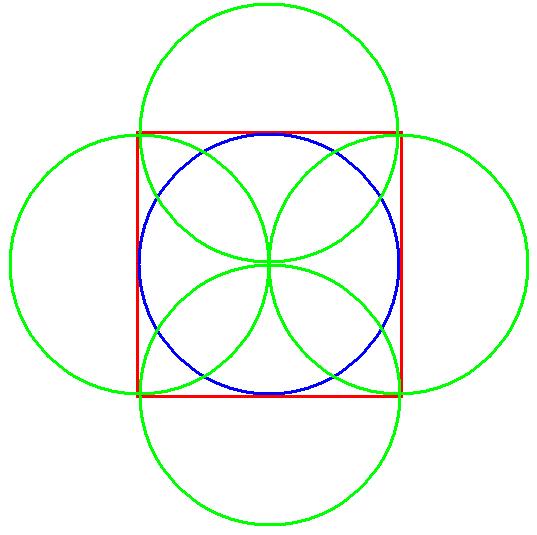
Putting the point of a compass half way up one side of the square draw a circle as below (shown in green). Repeat this three more times, once for each side of the square.
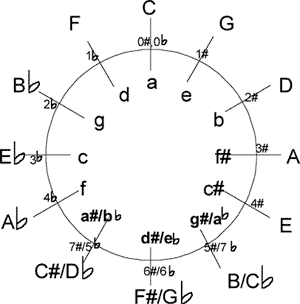
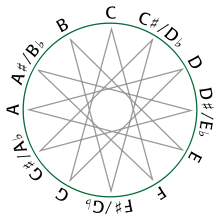
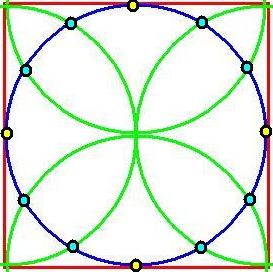
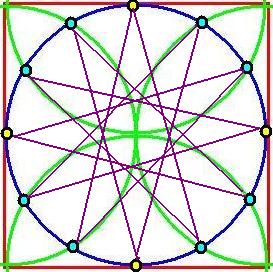
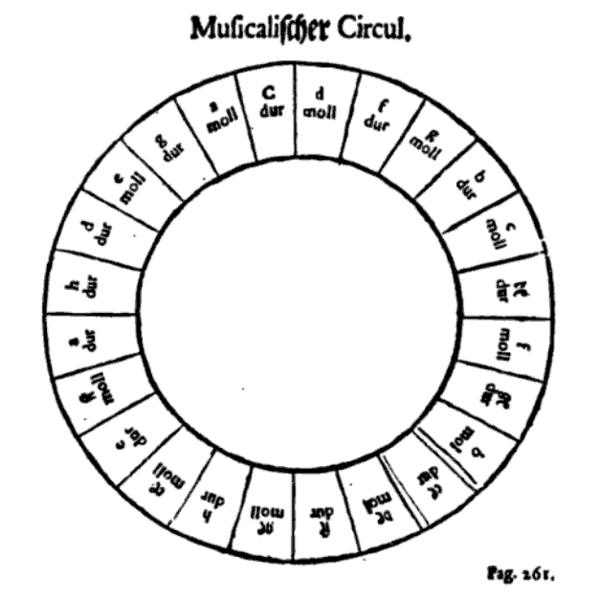
Now comes the clever bit. The first figure on the left,below, is a reduced version of the one above - in the middle drawing, add one dot to each point where the green semicircle crosses the blue circle (shown in light blue) and also where the red square impinges on the blue circle as in the middle picture, (shown as yellow dots). Next, starting at the one o’clock position, and counting clockwise, draw a line to a point, five dots around the clock face, to end up at the six o’clock position. From there repeat the operation always in the clockwise direction and always five points around the clock face, until all the dots are connected and you have the dodecagram, as in the third picture. You can see immediately that the number five is woven into the fabric of the dodecagram and this was obvious to Johann Heinichen when he devised his ‘circle of fifths’. In Western music an octave is divided into 12 parts, so he sought a way to include a musical fifth into the number 12 and the dodecagram is the answer. Even though he did not include the dodecagram in his design, it is clear from the method required to ‘read’ the circle of fifths that a dodecagram was a natural result of using it. Because one has to ‘read’ it by picking two points five units apart around the edge of the circle, divided into twelve parts. What could be more But Heinichen did not produce just the one design as in the far left drawing, but published another one later which looked like the one immediately adjacent. This was in 1728 and he called it a ‘Quintenzirkel’, or circle of fifths. As you can see they were both divided into 24 segments, indicating alternating major and minor keys, ‘dur’ and ‘moll’ respectively. Modern versions have changed the design but the method for reading the circle of fifths was the same then as it is now. See the modern picture underneath Heinichen’s one. A different circle of fifths is shown below, on the left. Major keys are shown around the outside of the circle. Minor keys are shown on the inside of the circle. The number of sharps or flats in each key are shown at each space, with C major and A minor (no sharps or flats) always at the top. The drawing on the right, below, is a modern version of Heinichens second drawing. Heinichen’s drawings place the major and minor keys around the same circle rather than separately around an inner circle as is shown left below. You can merge the 24 segments into twelve pairs, then you can pick a letter and count five points around the circle and join them with a line, and you have the beginnings of the dodecagram.
In my opinion the purpose of MT 137 is to point yet again to the number 5. I think that all attempts to wring some kind of mechanism from it are doomed. If the presence of the number five was not so prevalent in Bessler’s work I might agree that there must be some other explanation for MT 137, but the number pops up everywhere and I think this is just an example. Copyright © 2011 John Collins.
|
| NavB[Home] [Bessler's name code] [Apologia Pentagram] [AP chronogram] [AP blanks & dashes] [AP Chapter 55] [Bessler's Initials] [Portrait pentagram] [More 1st portrait] [2nd portrait] [Pentagram in GB] [Golden Mean] [MT 55 pentagram] [MT Nos & letters] [MT 137 part one] [MT 137 part two] [MT 137 part three] [Bessler's Logo] [Drawing no codes] [5th DT Drawing] [Water wheel]wing |
 natural than to
natural than to 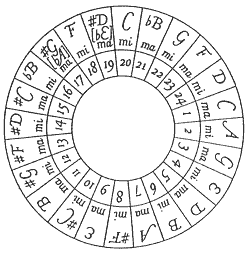 draw the lines between the two points identified - and do so for each point or note written around the circle’s edge?
draw the lines between the two points identified - and do so for each point or note written around the circle’s edge?