 |
|||
|
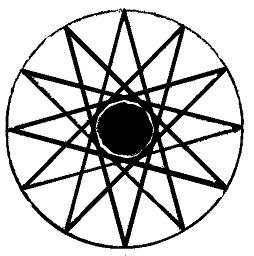
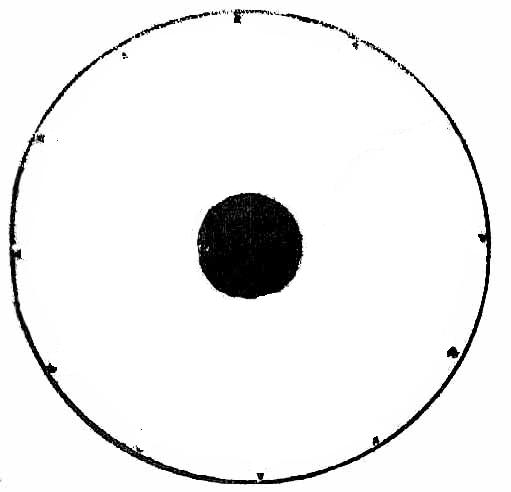
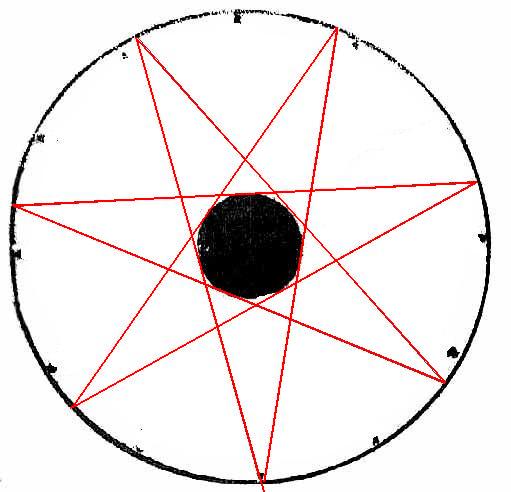
I explained my reasons for thinking that this drawing, Maschinen Tractate 137, was pointing to the ‘circle of fifths’ as described by Johann Heinichen, in MT 137 A. There is no opportunity to change or add any features to the drawing - it is precisely drawn as a dodecagram. I say there is no opportunity to alter the drawing but in fact there is one feature which to my mind is the beginning point of the solution. I refer to the black, filled-in circle in the centre which looks like it might represent the axle of a wheel. It does offer one possibility to my mind and that is as follows. If we look at the same figure with all the straight lines removed it looks like the left drawing below. It will be noticed in the original illustration that the black lines, while passing close to the inner black circle, do not actually touch it. They are also very thick lines which disguises the fact that they miss the edge of the circle. If we now fill in new lines only this time we allow them to graze the edge of the black centre ci Some may think that this is wishful thinking on my part and so I urge all who doubt, to copy the illustration on the left into MS Paint and test it for yourself. The proof is thoroughly convincing. If the lines go too far into the solid black circle they don’t meet at the circumference and if they go too wide they don’t converge within the circle at all. So why a seven sided polygon? Why, given his obsession with the number five, didn’t he use a decagram? At least that has ten sides and he could imply that there were two pentagrams in it. I think he had set his heart on using Heinichen’s circle of fifths, because its name held the clue to the secret of the number five and would be instantly recognisable to another musician. A decagram might have been too obvious so he chose the dodecagram but then as he usually did, he hid a second clue within it which would lead to another piece of information. By carefully including a solid black circle which was just the slightest bit too small it might attract the attention of someone searching for clues who would do exactly what I have done. It could easily have been done at the time by using oiled paper or a sheet of glass upon which to scribe the lines. It might be thoug But this does not explain why a seven-sided figure was chosen. In ‘Nos and letters’, I have discussed the variations deliberately employed by Bessler in numbering the drawings in Maschinen Tractate and I have suggested that the reason certain numbers were written in a different style was to reflect his belief that only odd numbers, and more than three, of mechanisms, would produce a working gravity wheel. Five was the optimum number because it allowed the most space for a fuller range of movement but seven and even nine mechanisms could produce potential working wheels. Therefore it is for this reason that I think that Bessler introduced the seven sided polygon - i.e., to inform us that seven mechanisms were acceptable in a working gravity wheel. It was the only polygon he could fit inside the dodecagram that agreed with his 5,7 or 9 mechanisms. Referring back to the ‘circle of fifths’, it is worth pointing out that the twelve tones are actually only made up of seven letters: A - B - C - D - E - F - G There are two versions of the heptagram - the obtuse and the acute. Bessler’s was an acute heptagram. The obtuse heptagram has been included in the drawing on the left, above, in blue to show the differences. Some definitions describe the obtuse polygon as the septagram and the acute one as the heptagram. Both names mean the same thing but one is Greek and the other Latin. The septagram has associations with magic and wicca, while the other, the heptagram, is more usually connected with the kabbalah; an interest shared by Bessler. The obtuse form suggests passivity, contentment and attuning with nature and its forces; The acute, active form suggests an outgoing interaction with nature's forces, making progressive use of them, which does seem to apply to a gravitywheel. In my opinion the inclusion of the heptagram is merely a repeat of Bessler’s other clues as discussed under the button marked MT numbers and is further proof that Bessler maintained that odd numbers of mechanisms of five or more were necessary for a successful gravitywheel. Recently I unearthed some more evidence that Bessler did indeed intend for us to assume that he was referring to the Circle of Fifths. Press the button marked MT137 C.
Copyright © 2009 John Collins.
|
| NavB[Home] [Bessler's name code] [Apologia Pentagram] [AP chronogram] [AP blanks & dashes] [AP Chapter 55] [Bessler's Initials] [Portrait pentagram] [More 1st portrait] [2nd portrait] [Pentagram in GB] [Golden Mean] [MT 55 pentagram] [MT Nos & letters] [MT 137 part one] [MT 137 part two] [MT 137 part three] [Bessler's Logo] [Drawing no codes] [5th DT Drawing] [Water wheel]wing |
 rcle we obtain a heptagram or septagram.
rcle we obtain a heptagram or septagram.
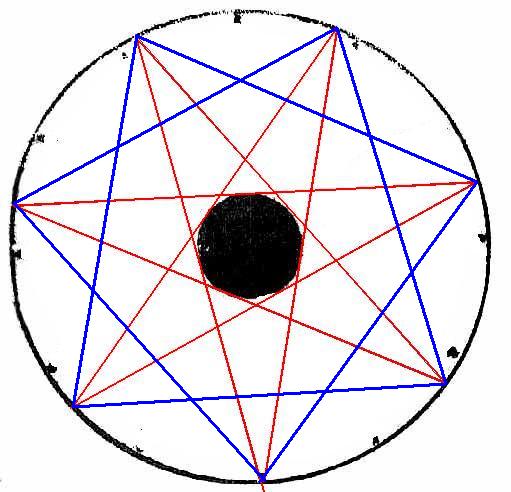 ht that Bessler would have somehow incorporated his beloved 5 or 55 within the dodecagram, but in fact if you try to draw a pentagram inside the same sized circle, the central black circle which you must then draw within its chords is too big to fit inside the lines in the above circle; and a bigger solid black circle would overlap the dodecagram vertices. If you try making the red lines pass just inside the edge of the black circle they do not meet at the circumference. Moreover, if the circle shown was a twelve foot diameter wheel, like the Kassel wheel, then the solid black circle which would represent its axle, would be about two and half feet wide not six inches as reported. As there seems no good reason for the inclusion of the slightly undersized solid black circle within the dodecagram, I am certain that the heptagram/septagram is intended to be found.
ht that Bessler would have somehow incorporated his beloved 5 or 55 within the dodecagram, but in fact if you try to draw a pentagram inside the same sized circle, the central black circle which you must then draw within its chords is too big to fit inside the lines in the above circle; and a bigger solid black circle would overlap the dodecagram vertices. If you try making the red lines pass just inside the edge of the black circle they do not meet at the circumference. Moreover, if the circle shown was a twelve foot diameter wheel, like the Kassel wheel, then the solid black circle which would represent its axle, would be about two and half feet wide not six inches as reported. As there seems no good reason for the inclusion of the slightly undersized solid black circle within the dodecagram, I am certain that the heptagram/septagram is intended to be found.